Pamiętam, że podczas uruchamiania nowych form wtryskowych bardzo często w dokumentacji technologicznej trzeba było zaznaczyć „TAK” przy zdaniu „Czy przeprowadzono optymalizację procesu?”. Nikt sobie wtedy chyba nie zdawał sprawy (łącznie ze mną), że nie da się odpowiedzieć na tak zadanie pytanie, a tym bardziej przeprowadzić optymalizację stojąc jedynie przez kilka godzin przy maszynie.
Co to jest optymalizacja?
Optymalizacja to dobór odpowiednich danych wejściowych procesu w celu uzyskania określonych wielkości wyjściowych tego procesu. Innymi słowy, optymalizacja polega na doborze warunków przetwórstwa, które spełniają wymagane zadanie produkcyjne, np. minimalizacji czasu cyklu.[1]
Zadanie to należy oczywiście uprzednio zdefiniować. Tak jak „nie ma miłości bez zazdrości”, tak nie ma optymalizacji bez jej kryteriów. Tego zabrakło we wspomnianym wyżej formularzu z prób formy. Bardzo często nie ma też tego w codziennej pracy na wtryskowni, gdzie kierownictwo po prostu nakazuje zoptymalizować produkcję.
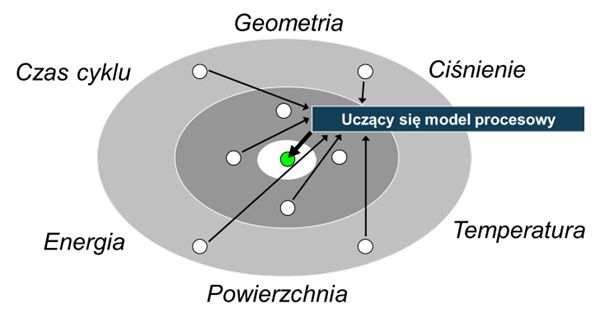
Optymalizacja procesu wtryskiwania tworzyw to złożone zagadnienie. Istnieje wiele różnych, często wzajemnie sprzecznych kryteriów optymalizacji, takich jak minimalizacja czasu chłodzenia przy jednoczesnej minimalizacji odkształceń wywołanych skurczem. Proces charakteryzuje się dodatkowo dużą liczbą zmiennych, obejmujących parametry materiałowe, specyfikację maszyny i narzędzia oraz warunki technologiczne. Wielkości te są również od siebie zależne. „Wszystko jest połączone” tak jak to pokazano rysunku poniżej.
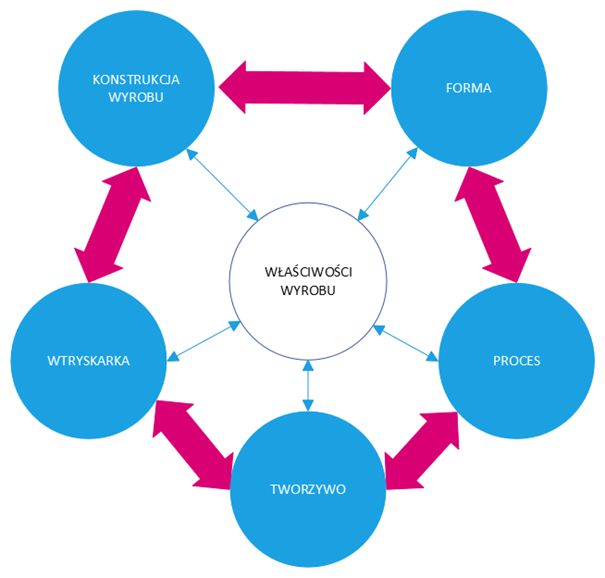
Metody optymalizacji
Za problem optymalizacji procesu wtryskiwania można się zabrać na kilka sposobów.
„Strzelanie do tarczy”
Najbardziej popularna jest chyba metoda w naszej rodzimej nomenklaturze nazywana „grupowym zmóżdżaniem się”, „metodą staro-egipską” lub po prostu metodą prób i błędów. Anglosasi zwykli na nią mawiać „gun shot”, co moim zdaniem najlepiej oddaje jej charakter. 😉
Każdy na pewno kojarzy poniższy obrazek, na którym ustawiacz, technolog, jakościowiec i kierownik produkcji wspólnie „optymalizują” proces. Każdy z nich testuje swoje pomysły na rozwiązanie problemu. Na końcu wybierany jest jeden, bardzo często wcale nie ten obiektywnie najlepszy.
Przypomina to właśnie takie strzelanie do tarczy. Każdy oddaje swój strzał. Niestety nie wiemy jak dokładnie wygląda tarcza – nie znamy optymalnego punktu pracy wtryskarki, więc trudno jest nam ocenić kto był najbliżej jej środka. Dlatego nasz końcowy wybór podejmowany jest „na wyczucie” i zwykle bywa daleki od optymalnego. Jest to najmniej skuteczna metoda.

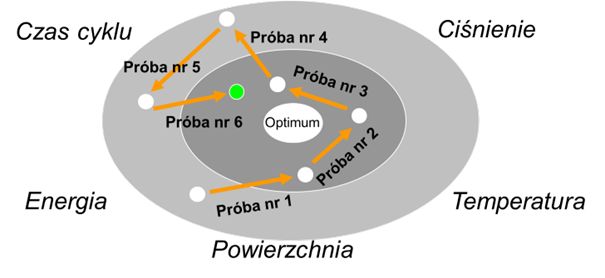
Metoda statystyczna
Metody te umożliwiają utworzenie wielowymiarowej przestrzeni wielkości wyjściowych procesu (przestrzeni odpowiedzi) na podstawie przygotowanych zestawów danych wejściowych, a następnie identyfikację wartości ekstremalnych (minimów lub maksimów) w tej przestrzeni. Dane niezbędne do optymalizacji można pozyskiwać dwojako: poprzez badania eksperymentalne procesu (próby technologiczne) lub za pomocą symulacji komputerowych. Pierwszy sposób jest kosztowny i ograniczony zakresem dostępnych danych. Dlatego obecnie kluczowe znaczenie ma optymalizacja oparta na danych uzyskiwanych w wyniku symulacji procesu.
Wracając do analogii ze strzelaniem do celu, tutaj oddajemy nasze strzały w bardziej zorganizowany i zaplanowany sposób (DoE – Design of Experiment, czyli planujemy próby), zazwyczaj pokrywając większy obszar tarczy strzelniczej. Teraz mamy dużo wyższe szanse na trafienie w jej środek, albo przynajmniej w miejsce gdzieś w jego pobliżu.
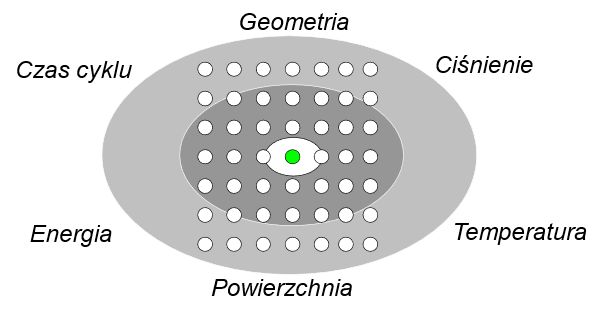
Celem samego planowania doświadczeń (DoE) jest maksymalizacja ilości informacji o badanym zjawisku przy jednoczesnej minimalizacji liczby koniecznych pomiarów. Metody te pozwalają odpowiedzieć na dwa fundamentalne pytania:
- w jaki sposób optymalnie zaplanować doświadczenie,
- jak prawidłowo analizować uzyskane wyniki badań.
Sztuczna inteligencja
Modelowanie i optymalizacja procesów wtryskiwania może być również realizowana za pomocą technik obliczeniowych sztucznej inteligencji (Computational Intelligence), takich jak sieci neuronowe i algorytmy genetyczne.
W tym podejściu zaczynamy, podobnie jak w przypadku metod statystycznych od planowania eksperymentu i przeprowadzenia prób wtryskiwania (wirtualnych i/lub rzeczywistych). Tym razem nie wybieramy z zestawu otrzymanych danych tych najlepszych – optymalnych, a wykorzystujemy je do zbudowania numerycznego modelu procesu, np. ucząc sieć neuronową.
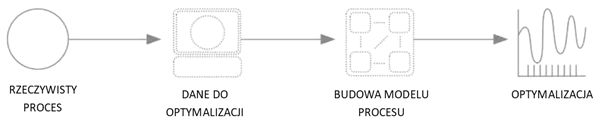
Dopiero ta wyuczona sieć neuronowa strzela do tarczy i ponieważ jest taka mądra (w kwestii znajomości konkretnego procesu mądrzejsza od nas) trafia w dziesiątkę.
Model procesu może przybierać postać przestrzeni zamieszkałej przez określoną populację osobników. Osobniki te reprezentują zakodowane w formie chromosomów zbiory parametrów zadania, które stanowią punkty w przestrzeni poszukiwań, na przykład parametry procesu wtryskiwania. Chromosom to uporządkowany ciąg znaków (genów), a struktura złożona z zespołu chromosomów tworzy genotyp osobnika, reprezentujący zestaw kilku parametrów wtryskiwania, takich jak prędkość wtrysku, ciśnienie docisku czy temperatura formy.
Proces rozpoczyna się od wylosowania populacji początkowej, która podlega ocenie na podstawie wartości funkcji przystosowania (celu). Funkcją celu może być na przykład minimalizacja wypaczenia wypraski. Najlepiej przystosowane osobniki, które generują najwyższe wartości funkcji celu, uczestniczą w procesie reprodukcji. Ich genotypy podlegają operacjom genetycznym: krzyżowaniu (wymianie fragmentów chromosomów) oraz mutacji (wprowadzaniu drobnych, losowych zmian w genotypie). W efekcie powstaje druga generacja, która również podlega ocenie, a cała procedura jest powtarzana aż do osiągnięcia wystarczająco dobrego rozwiązania.
Optymalizacja w praktyce produkcyjnej
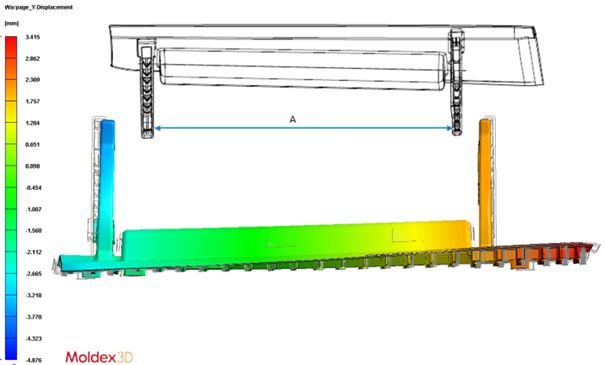
Teraz przyszedł czas aby pokazać jak to wszystko działa na przysłowiowej hali produkcyjnej. Na warsztat weźmiemy wypraskę z branży samochodowej wykonaną z niewzmocnionego polipropylenu. Problemem do rozwiązania jest zbyt mała, niemieszcząca się w tolerancji wykonania wartość wymiaru A zaznaczona na rysunku poniżej.
Wyznaczenie okna optymalizacji
Pod nazwą okna optymalizacji kryją się wartości kryteriów i parametrów optymalizowanych. W tym konkretnym przypadku jedynym kryterium jest minimalna wartość odchyłki wymiaru A (jak najbliższa 0), a parametrami są:
- temperatura wtrysku,
- temperatura formy,
- czas docisku,
- ciśnienie docisku,
- prędkość wtrysku (natężenie przepływu).
Planowanie i przeprowadzenie prób
Kolejnym etapem jest rozpisanie DoE, czyli planu eksperymentu. Tutaj posłużono się metodą macierzy ortogonalnych Taguchiego do stworzenia listy dwunastu prób, a następnie przeprowadzono symulacje wtryskiwania w programie Moldex3D. Otrzymane wyniki w postaci wartości odchyłki wymiaru A zostały poddane analizie metodą statystyczną i posłużyły do zbudowania modelu procesu w postaci sieci neuronowej.
| Lp. | Temperatura wtrysku [°C] | Temperatura formy [°C] | Czas docisku [s] | Max. wartość ciśnienia docisku [%] | Max. wartość profilu natężenia przepływu [%] |
| 1 | 210 | 20 | 5 | 33 | 33 |
| 2 | 210 | 20 | 5 | 33 | 33 |
| 3 | 210 | 20 | 15 | 100 | 100 |
| 4 | 210 | 60 | 5 | 100 | 100 |
| 5 | 210 | 60 | 15 | 33 | 100 |
| 6 | 210 | 60 | 15 | 100 | 33 |
| 7 | 270 | 20 | 15 | 100 | 33 |
| 8 | 270 | 20 | 15 | 33 | 100 |
| 9 | 270 | 20 | 5 | 100 | 100 |
| 10 | 270 | 60 | 15 | 33 | 33 |
| 11 | 270 | 60 | 5 | 100 | 33 |
| 12 | 270 | 60 | 5 | 33 | 100 |
Wyniki optymalizacji
Poniższa tabela pokazuje zestawienie wyników optymalizacji i chyba też przekonuje, że optymalizować zawsze warto.
| Przed optymalizacją | Optymalizacja statystyczna (Moldex3D Expert) | Optymalizacja sieciami neuronowymi | |
| Wartość odchyłki wymiaru A [mm] | 4,77 | 2,93 | 1,90 |
Podsumowanie
Warunkiem prawidłowego i świadomego prowadzenia procesu wtryskiwania jest zrozumienie zależności między parametrami ustawianymi na maszynie a właściwościami wyprasek. Pełne poznanie tych relacji pozostaje jednak praktycznie nieosiągalne ze względu na niezwykłą złożoność procesów przetwórstwa tworzyw sztucznych.
W tej sytuacji niezbędne stają się narzędzia analityczne, które umożliwiają efektywne zarządzanie wieloma zmiennymi procesowymi i ocenę ich wpływu na jakość produktu końcowego. Kluczową rolę odgrywają tu techniki optymalizacyjne, zarówno statystyczne jak i oparte na sztucznej inteligencji, wspierane przez symulacje wtryskiwania.
Dzięki zintegrowanemu zastosowaniu tych narzędzi nawet najbardziej problematyczne aspekty produkcji, takie jak wypaczenia i niezgodności wymiarowe produkowanych elementów, mogą zostać skutecznie kontrolowane i korygowane, prowadząc do satysfakcjonujących rezultatów.
Zapraszamy również do przeczytania:
Jak wygląda projektowanie form wtryskowych
Dlaczego warto przenieść produkcję z tworzyw sztucznych
Bibliografia
- Wilczyński K. (red.): Komputerowe wspomaganie projektowania w przetwórstwie tworzyw sztucznych, OWPW, Warszawa 2016
- Jakość i powtarzalność produkcji w przetwórstwie tworzyw, Postawa P., Cichoń B. Tworzywa Sztuczne w Przemyśle 1/2012
- Łomotowska Ż.: Optymalizacja procesu wtryskiwania wg kryterium minimalnych wypaczeń wypraski, praca dyplomowa, Politechnika Warszawska 2019
- https://moldiverse.com
Autor: dr inż. Przemysław Narowski – Politechnika Warszawska
Od prawie 20 lat gromadzi doświadczenie w technikach wtryskiwania, pracując na stanowiskach ustawiacza, technologa, konstruktora form, inżyniera ds. symulacji i obliczeń, a także naukowca.
- Adiunkt w Zakładzie Przetwórstwa Tworzyw Sztucznych Politechniki Warszawskiej
- Doradca techniczny (ponad 30 konsultowanych firm)
- Certified Moldex3D Professional®
- Zwycięzca międzynarodowego konkursu Moldex3D Global Innovation Talent Award
- Specjalista w dziedzinie komputerowego wspomagania procesów przetwórstwa tworzyw sztucznych



